70以上 三角形と比 250603-三角形と比 証明

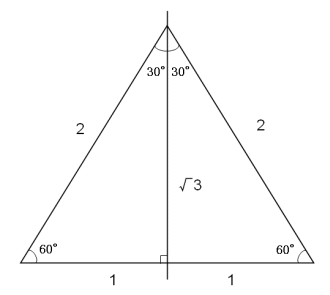
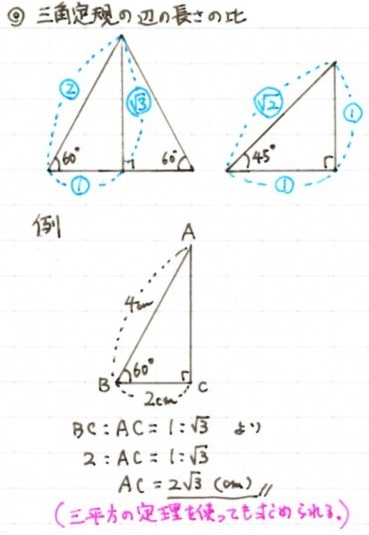
テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア
15 ∘ とその周辺の三角比の解答 75 ∘ = 90 ∘ − 15 ∘ であるから、 90 ∘ − A の三角比より次のように求めることができる。 105 ∘ = 90 ∘ 15 ∘ であるから、 90 ∘ θ の三角比より次のように求めることができる。 165 ∘ = 180 ∘ − 15 ∘ であるから、 180 ∘ あとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。 三角形 ABC の面積を S とすると、 $\mathrm{ BD }\mathrm{ DC }=54$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。
三角形と比 証明
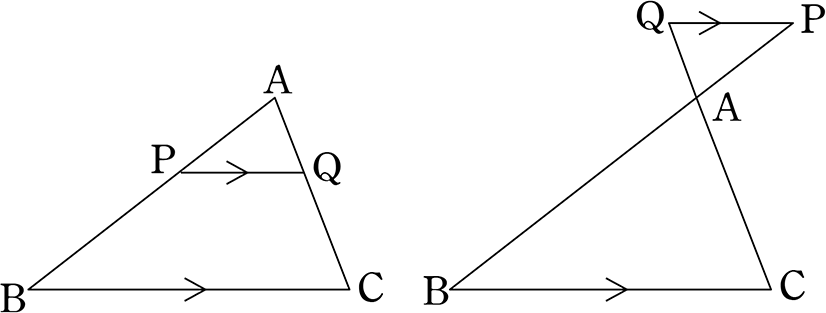
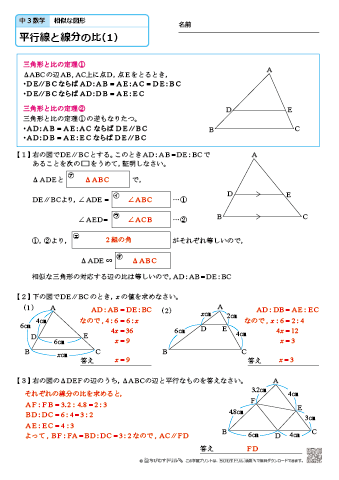
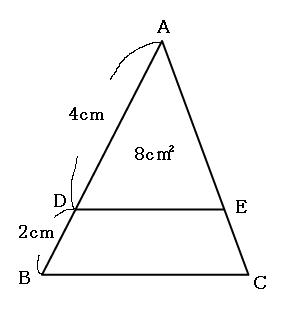
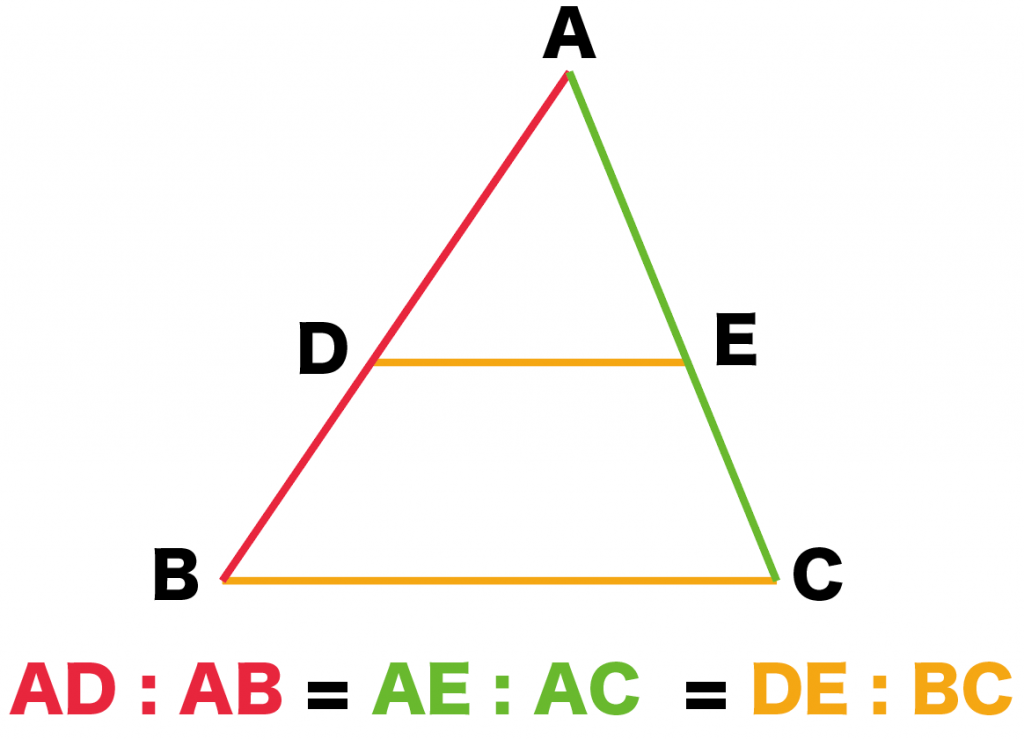
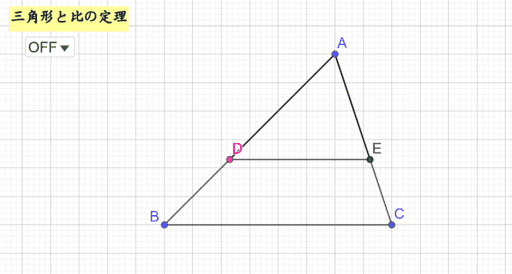
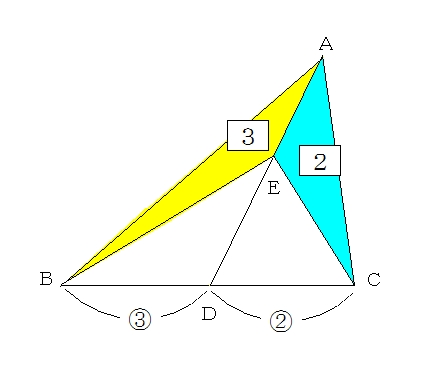
三角形と比 証明-こちらの記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。要点3 三角形の角の二等分線と比 三角形の角の二等分線について,次のことが成り立つ。 三角形の角の二等分線と比 ① abc の∠a の二等分線と辺bcとの交点を dとすると,dはbcをab:ac に内分する。 つまり bd:dc=ab:ac
1
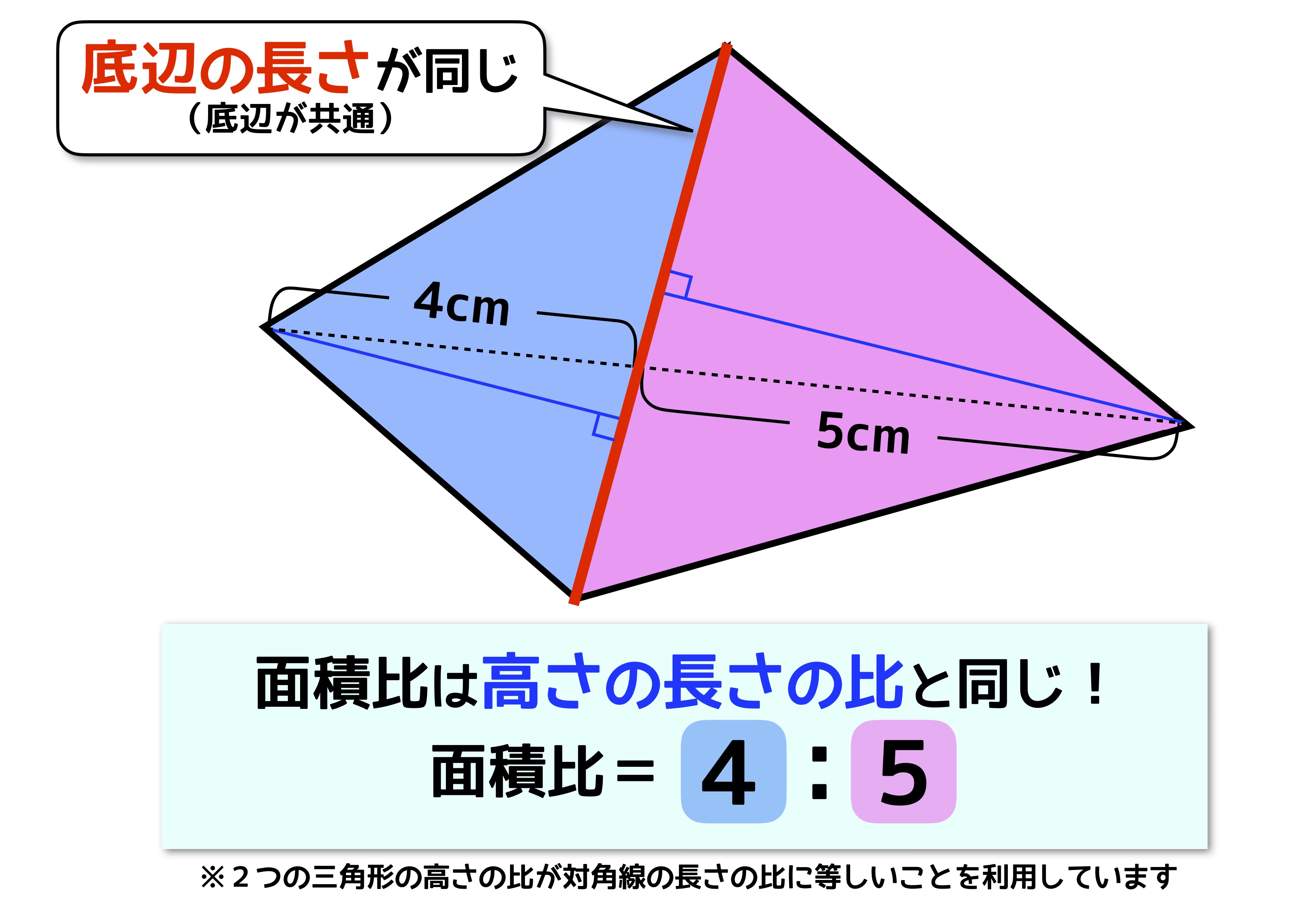
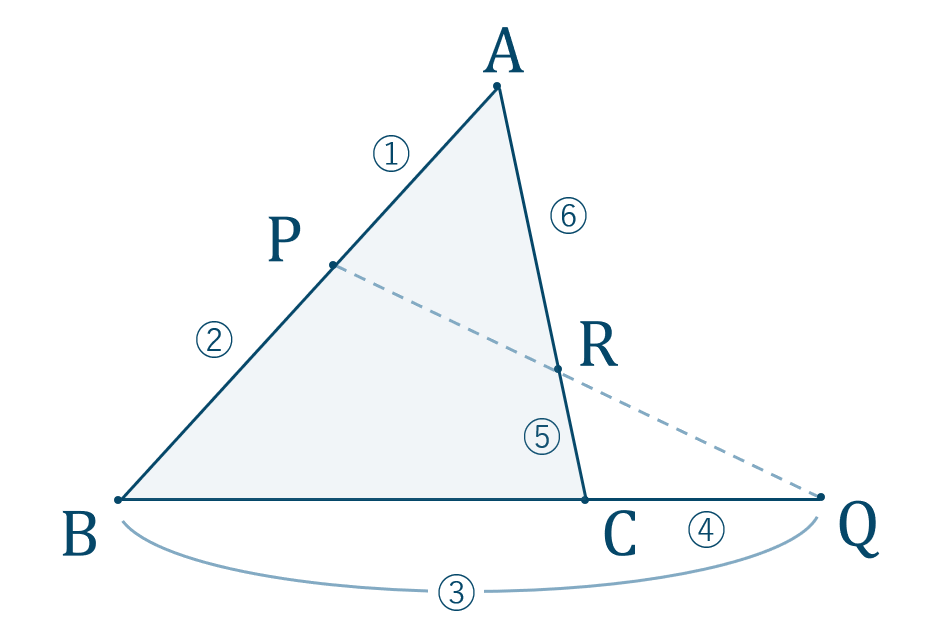
三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページつまり、 相似比 a b a b の図形の面積の比は a2 b2 a 2 b 2 です。 なので 面積の比は a×a b×b a × a b × b となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも 相似な図形ならば、面積比は相似比の 2 2 乗の比が成り立ちます。 二等分線を含む三角形の公式たち これら3つの公式を使うことで, 「二等分線を含む三角形について情報が3つ与えられれば残りの情報は全て求まる」 ことが分かります。 例 ( a, b, f) (a,b,f) (a,b,f) が分かれば公式2により cos A 2 \cos \dfrac {A} {2} cos 2A が
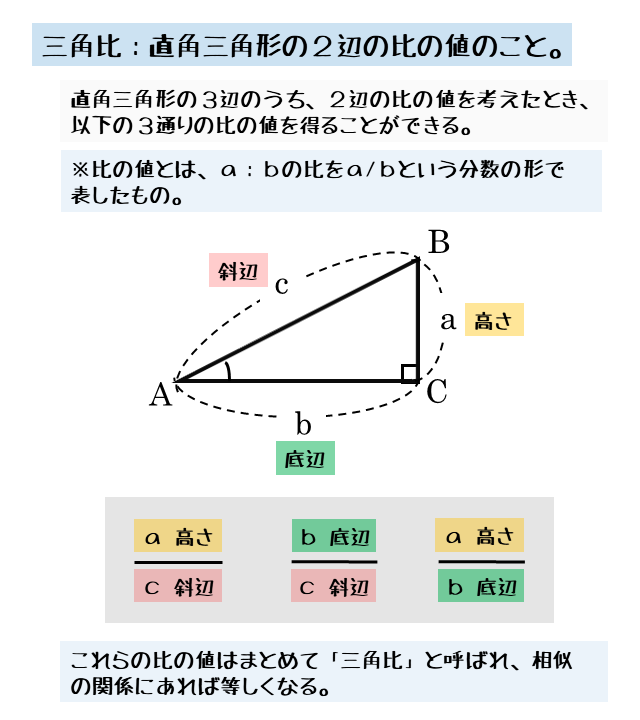
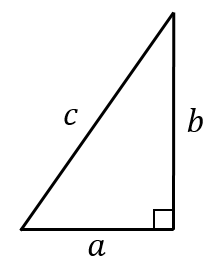
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です。 個人的には一番使う回数が多いと感じまし 三角比とは何か。その歴史と成り立ち 三角比の授業では、いちばんはじめに上の図のような定義を習います。 つまり直角三角形の3辺の長さをそれぞれ \(a\)、\(b\)、\(c\)として、左下の角度をθ(シータと読みます)とすると、
三角形と比 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 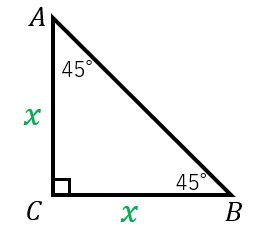 |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
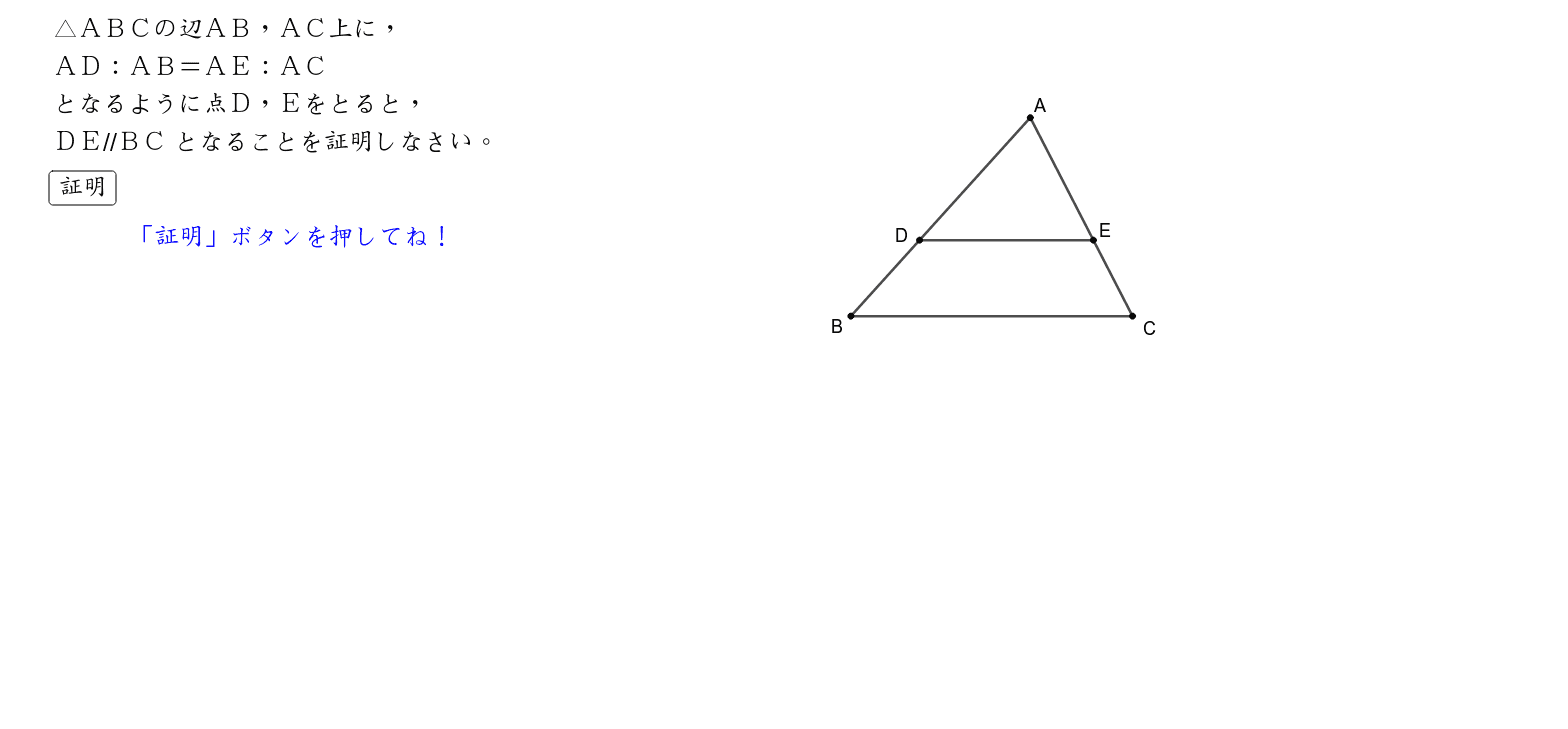 |  | |
 | ||
 |  | |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 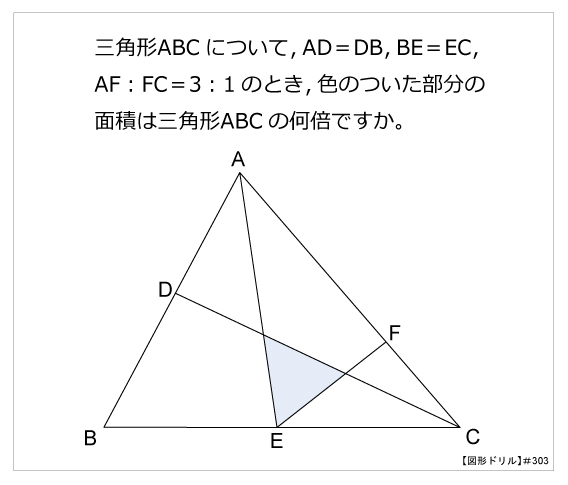 | |
 |  |  |
 | 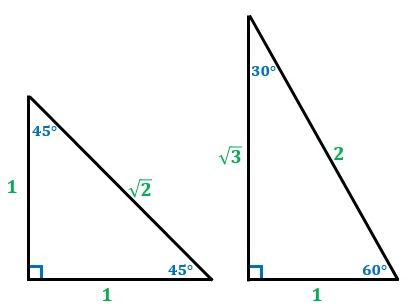 | 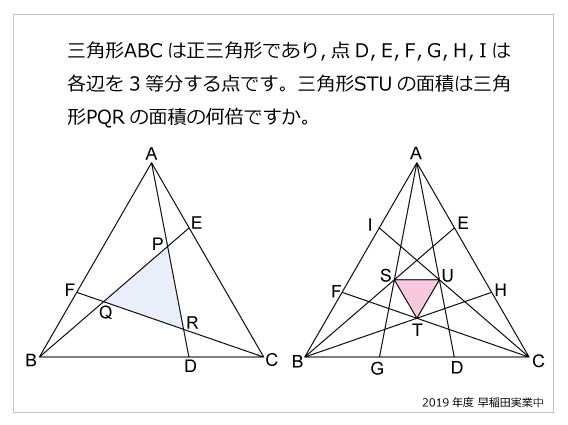 |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 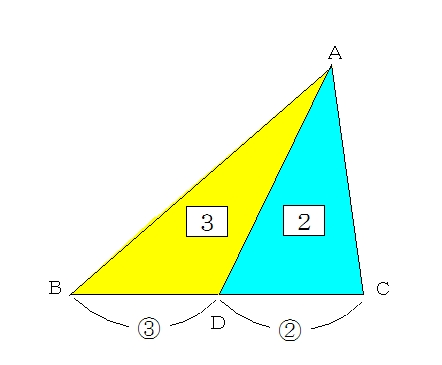 |
 |  |  |
 |  | |
「三角形と比 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
実は、 1つの角が等しい三角形の面積比は、その角をはさむ2辺の積によって求められます。 abc: ade=ab×ac:ad×aeと覚えておきましょう。 三角形の面積比のまとめ ここまで、三角形の面積比について解説してきました。 三角形の左側に注目すると、 abeと bdeは「高さが同じ隣り合う三角形」であることがわかります。 ①の型に該当するので、2つの面積比は底辺比に等しい。つまり abe: bde=2:1となる
Incoming Term: 三角形と比, 三角形と比の定理の逆, 三角形と比の定理の逆 証明, 三角形と比 証明, 三角形と比 問題, 三角形と比の定理とは, 三角形と比 中学, 三角形と比の定理の証明, 三角形と比の定理 問題, 三角形と比の定理 指導案, 三角形と比導入,
コメント
コメントを投稿